Νέος αλγόριθμος αλλάζει τους κανόνες και βρίσκει ταχύτερα τις συντομότερες διαδρομές

Ένα από τα πιο κλασικά προβλήματα της πληροφορικής, η εύρεση της συντομότερης διαδρομής μέσα σε ένα δίκτυο, απέκτησε πρόσφατα μια επαναστατική λύση. Μια ερευνητική ομάδα ανέπτυξε έναν αλγόριθμο που υπερβαίνει το θεωρητικά ανυπέρβλητο «όριο ταξινόμησης», καταφέρνοντας να εντοπίζει τις πιο σύντομες διαδρομές γρηγορότερα από οποιαδήποτε προηγούμενη μέθοδο, συμπεριλαμβανομένης της ιστορικής μεθόδου του Edsger Dijkstra.

Το κλασικό πρόβλημα των συντομότερων διαδρομών

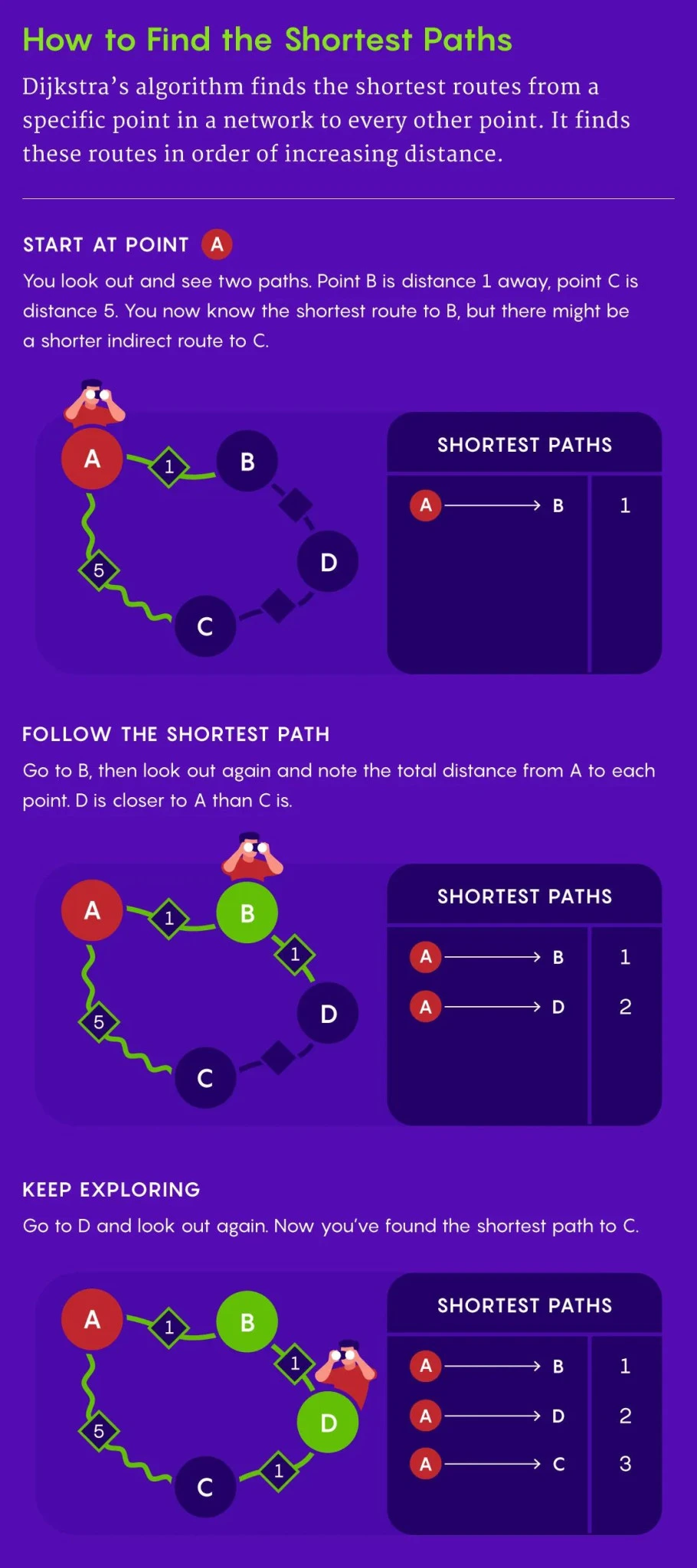
Στην ουσία, το ζήτημα αφορά τον εντοπισμό της ταχύτερης ή συντομότερης πορείας από ένα σημείο εκκίνησης προς όλα τα υπόλοιπα σημεία ενός δικτύου —όπως θα έκανε κάποιος που μόλις μετακόμισε και θέλει να μάθει τη βέλτιστη διαδρομή για τη δουλειά, το γυμναστήριο ή το σούπερ μάρκετ. Για να το μελετήσουν μαθηματικά, οι επιστήμονες χρησιμοποιούν τα λεγόμενα «γραφικά δίκτυα» (graphs), όπου οι κόμβοι συνδέονται με γραμμές που φέρουν βάρη, δηλαδή αριθμητικές τιμές που αντιπροσωπεύουν χρόνο ή απόσταση.

Το 1956, ο Dijkstra πρότεινε έναν αλγόριθμο που άλλαξε ριζικά τον τρόπο προσέγγισης του προβλήματος. Ο αλγόριθμός του λειτουργεί βήμα προς βήμα: ξεκινά από την πηγή και υπολογίζει τη συντομότερη διαδρομή προς τους πιο κοντινούς κόμβους, επεκτείνοντας σταδιακά το πεδίο αναζήτησης. Ωστόσο, η μέθοδός του βασίζεται στην ταξινόμηση των κόμβων ανάλογα με την απόσταση, μια διαδικασία που επιβάλλει έναν θεμελιώδη χρονικό περιορισμό. Όπως είχε δείξει η έρευνα πριν από τέσσερις δεκαετίες, κανένας αλγόριθμος που βασίζεται στην ταξινόμηση δεν μπορεί να ξεπεράσει αυτό το όριο ταχύτητας.

Η πρόκληση του «φράγματος ταξινόμησης»

Το 1984, ο Robert Tarjan και συνεργάτες του τελειοποίησαν τον αλγόριθμο Dijkstra ώστε να φτάσει ακριβώς σε αυτό το θεωρητικό όριο. Όποια προσπάθεια για περαιτέρω βελτίωση θα απαιτούσε μια μέθοδο που να αποφεύγει πλήρως την ταξινόμηση, κάτι που για δεκαετίες θεωρήθηκε αδύνατο.

Τις δεκαετίες του 1990 και 2000, ο Mikkel Thorup από το Πανεπιστήμιο της Κοπεγχάγης και άλλοι ερευνητές επιχείρησαν να σπάσουν το φράγμα αυτό, καταφέρνοντας μερικές επιτυχίες μόνο σε ειδικές περιπτώσεις, όπου τα βάρη των συνδέσεων ακολουθούσαν συγκεκριμένους κανόνες. Όμως μια γενική λύση φαινόταν ανέφικτη μέχρι που ο Ran Duan, καθηγητής στο Tsinghua University του Πεκίνου, αποφάσισε να αμφισβητήσει τα καθιερωμένα.

Ο Ran Duan και η ιδέα που άλλαξε τα δεδομένα

Το ενδιαφέρον του Duan για το πρόβλημα ξεκίνησε πριν από σχεδόν είκοσι χρόνια, όταν ως φοιτητής μεταπτυχιακού στο University of Michigan ασχολήθηκε με παραλλαγές του αλγορίθμου Dijkstra. Το 2021, διατύπωσε μια νέα προσέγγιση: αντί να εξετάζει κάθε κόμβο της «περιοχής μετώπου» (frontier), το σύνολο των κόμβων που βρίσκονται στο όριο της αναζήτησης, πρότεινε να ομαδοποιούνται οι γειτονικοί κόμβοι σε συστάδες. Από κάθε συστάδα θα επιλέγεται μόνο ένας αντιπροσωπευτικός κόμβος, μειώνοντας δραστικά τον αριθμό των υπολογισμών.

Αυτή η μέθοδος σήμαινε ότι ο αλγόριθμος δεν θα ακολουθούσε πάντα την απόλυτα συντομότερη διαδρομή με τη σειρά, αποφεύγοντας έτσι τον περιορισμό της ταξινόμησης. Η πρόκληση, ωστόσο, ήταν να αποδειχθεί ότι η νέα διαδικασία όντως οδηγεί σε ταχύτερη επίλυση χωρίς απώλεια ακρίβειας.

Από την ιδέα στην επιτυχία

Το φθινόπωρο του 2022, ο Duan συγκρότησε μια ομάδα τριών μεταπτυχιακών φοιτητών για να τελειοποιήσει την ιδέα. Οι πρώτες δοκιμές έδειξαν ότι η μέθοδός τους μπορούσε να «σπάσει» το φράγμα ταξινόμησης, αλλά μόνο για αμφίδρομα γραφήματα (undirected graphs), όπου κάθε σύνδεση λειτουργεί και προς τις δύο κατευθύνσεις.

Το επόμενο βήμα ήταν η εφαρμογή της ιδέας και σε κατευθυνόμενα γραφήματα (directed graphs), τα οποία είναι πολύ πιο περίπλοκα, αφού οι διαδρομές μπορεί να ισχύουν μόνο προς μία κατεύθυνση. Τότε ήταν που στο προσκήνιο εμφανίστηκε ο Xiao Mao, φοιτητής στο Stanford University, ο οποίος άκουσε τον Duan να παρουσιάζει τα αποτελέσματά του σε συνέδριο στην Καλιφόρνια το καλοκαίρι του 2023 και αποφάσισε να συνεργαστεί μαζί του.

Η ομάδα εμπνεύστηκε από τον παλιό αλγόριθμο Bellman-Ford, γνωστό για την αξιοπιστία του αλλά και για τη βραδύτητά του. Ο Duan και οι συνεργάτες του βρήκαν τρόπο να αξιοποιήσουν μόνο ορισμένα στάδια του Bellman-Ford, έτσι ώστε να επιλέγουν πιο «στρατηγικούς» κόμβους, εκείνους που συνδέονται με πολλές άλλες κρίσιμες διαδρομές στο δίκτυο. Έτσι, ο νέος αλγόριθμος απέκτησε τη δυνατότητα να «προβλέπει» ποιοι κόμβοι αξίζει να εξερευνηθούν πρώτοι, επιταχύνοντας σημαντικά τη διαδικασία.

Το 2024, ο Mao πρότεινε μια βελτιωμένη εκδοχή που απέφευγε τη χρήση τυχαιότητας, κάτι που οι επιστήμονες πάντα επιδιώκουν για μεγαλύτερη αξιοπιστία. Ο Duan, ανατρέχοντας σε μια τεχνική που είχε αναπτύξει ήδη από το 2018, συνδύασε όλες τις ιδέες σε ένα ολοκληρωμένο σύστημα. Το αποτέλεσμα ήταν ένας αλγόριθμος που ξεπερνά τον Dijkstra τόσο σε κατευθυνόμενα όσο και σε αμφίδρομα γραφήματα.

Ένα νέο κεφάλαιο για την επιστήμη των αλγορίθμων

Ο νέος αλγόριθμος λειτουργεί με «στρώσεις» – προχωρά προς τα έξω από το αρχικό σημείο, όπως και ο Dijkstra, αλλά αντί να ταξινομεί όλους τους κόμβους, χρησιμοποιεί μια δυναμική μέθοδο επιλογής βασισμένη σε κρίσιμα σημεία του γραφήματος. Έτσι, αποφεύγει τον περιορισμό της ταξινόμησης και επιτυγχάνει ταχύτερους χρόνους.

Όπως σχολίασε ο Mikkel Thorup, «αυτό το αποτέλεσμα είναι εντυπωσιακό, όχι μόνο γιατί σπάει ένα θεωρητικό όριο, αλλά γιατί βασίζεται σε ιδέες που θα μπορούσαν να είχαν ανακαλυφθεί πριν από δεκαετίες».

Η ομάδα του Duan σχεδιάζει να βελτιώσει περαιτέρω τον αλγόριθμο και να διερευνήσει αν υπάρχει ακόμη περιθώριο επιτάχυνσης. Όπως υποστηρίζει ο Robert Tarjan, «το φράγμα της ταξινόμησης μπορεί να έπεσε, αλλά αυτό δεν σημαίνει ότι έχουμε φτάσει στο τέλος του δρόμου».

[via]