Ήταν 10 Ιουνίου του 1854. Στο Πανεπιστήμιο του Γκέτινγκεν, ένας νεαρός και εξαιρετικά αγχωμένος μαθηματικός, ο Μπέρναρντ Ρίμαν, ανέβαινε στο βήμα για να δώσει τη διάλεξη που θα έκρινε την ακαδημαϊκή του καριέρα. Στο ακροατήριο καθόταν ο μέντοράς του, ο θρυλικός Καρλ Φρίντριχ Γκάους. Το θέμα που είχε επιλεγεί σχεδόν τυχαία, «Περί των υποθέσεων που κείνται στα θεμέλια της Γεωμετρίας», έμελλε να μην είναι απλώς μια τυπική παρουσίαση, αλλά η στιγμή που η ανθρωπότητα απέκτησε τα εργαλεία για να κατανοήσει το σχήμα του Σύμπαντος.
Εκείνη την ημέρα γεννήθηκε η έννοια της «πολλαπλότητας» (manifold). Μια ιδέα τόσο ριζοσπαστική που χρειάστηκαν δεκαετίες για να βρει την πλήρη εφαρμογή της στη φυσική, αλλά που σήμερα αποτελεί τον ακρογωνιαίο λίθο για τα πάντα: από τη Γενική Σχετικότητα του Αϊνστάιν μέχρι τη Θεωρία των Χορδών και την ανάλυση μεγάλων δεδομένων (Big Data).
Η «απόδραση» από τη φυλακή του Ευκλείδη
Για περισσότερα από 2.000 χρόνια, η μαθηματική σκέψη ήταν εγκλωβισμένη στους κανόνες του Ευκλείδη. Ο κόσμος θεωρούνταν επίπεδος, άκαμπτος και υπάκουε σε αυστηρούς κανόνες: οι παράλληλες γραμμές δεν τέμνονταν ποτέ και το άθροισμα των γωνιών ενός τριγώνου ήταν πάντα 180 μοίρες. Αυτή η «επίπεδη» γεωμετρία λειτουργούσε άψογα για αρχιτέκτονες και μηχανικούς, αλλά απέτυχε να περιγράψει την πολυπλοκότητα ενός καμπύλου κόσμου.
Ο Ρίμαν τόλμησε να σκεφτεί διαφορετικά. Πρότεινε μια νέα θεώρηση όπου ο χώρος δεν είναι ένα στατικό κουτί, αλλά μια δυναμική οντότητα που μπορεί να καμπυλωθεί, να τεντωθεί και να έχει οποιαδήποτε διάσταση.
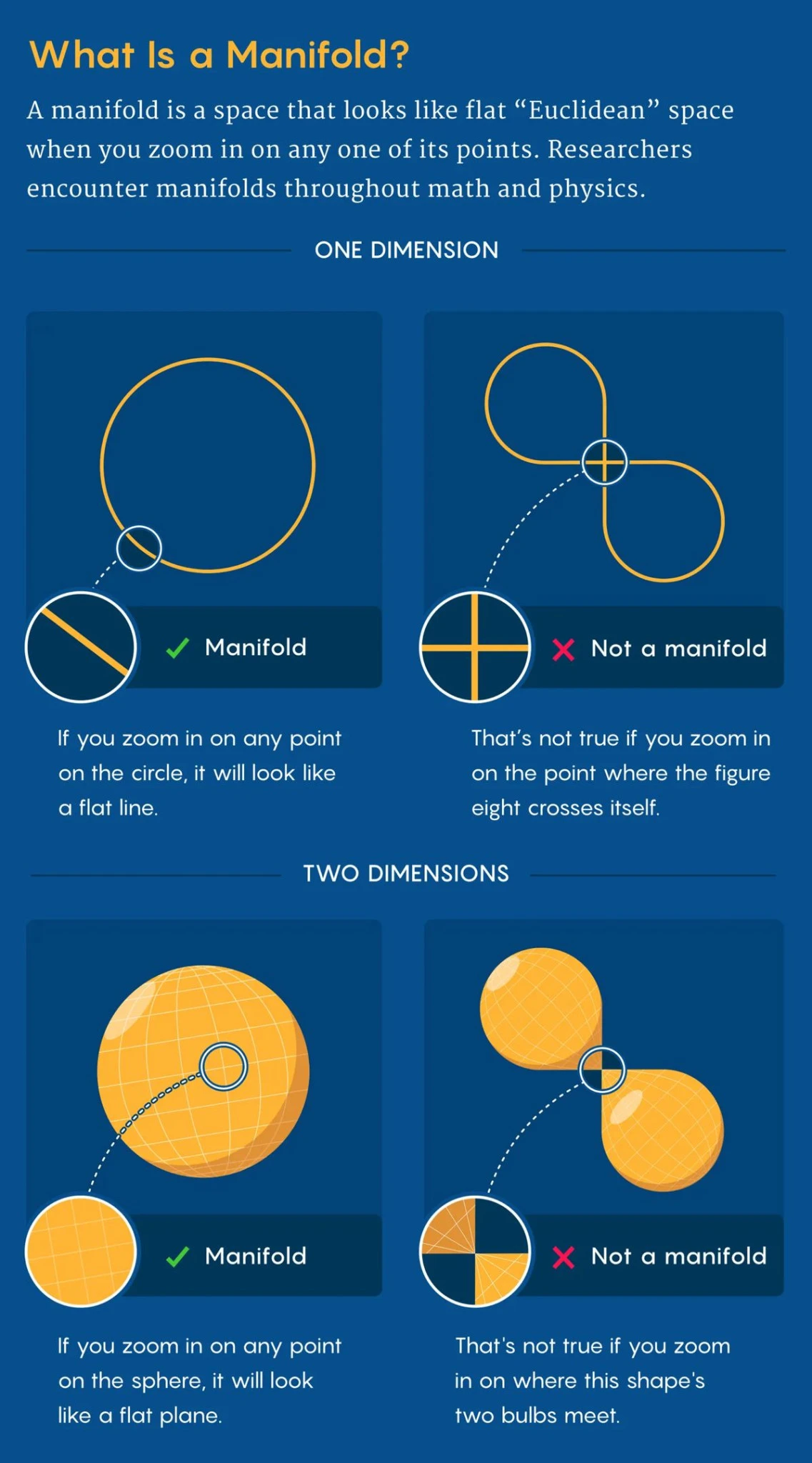
Εδώ μπαίνει η έννοια της πολλαπλότητας. Φανταστείτε ένα μυρμήγκι που περπατάει πάνω σε μια μεγάλη μπάλα. Για το μυρμήγκι, η περιοχή γύρω του μοιάζει επίπεδη. Αν ζωγραφίσει ένα μικρό τρίγωνο, αυτό θα υπακούει στους κανόνες του Ευκλείδη. Ωστόσο, αν το μυρμήγκι συνεχίσει να περπατάει, θα επιστρέψει στο σημείο που ξεκίνησε, αποδεικνύοντας ότι ο «κόσμος» του δεν είναι επίπεδος, αλλά σφαιρικός.
Μια πολλαπλότητα, λοιπόν, είναι ένας χώρος που μπορεί να έχει περίπλοκο σχήμα στο σύνολό του, αλλά αν εστιάσουμε σε ένα πολύ μικρό κομμάτι του (τοπικά), μοιάζει με τον γνωστό, επίπεδο Ευκλείδειο χώρο. Αυτή η ιδιοφυής απλούστευση επέτρεψε στους μαθηματικούς να χρησιμοποιούν τα οικεία εργαλεία του λογισμού και της άλγεβρας σε αντικείμενα αδιανόητης πολυπλοκότητας.
Το δώρο του Ρίμαν στον Αϊνστάιν
Η πραγματική δύναμη της πολλαπλότητας αποκαλύφθηκε σχεδόν 60 χρόνια μετά τη διάλεξη του Ρίμαν. Όταν ο Άλμπερτ Αϊνστάιν πάλευε να διατυπώσει τη Γενική Θεωρία της Σχετικότητας, συνειδητοποίησε ότι του έλειπε η κατάλληλη μαθηματική γλώσσα για να περιγράψει τη βαρύτητα. Η βαρύτητα δεν ήταν μια αόρατη δύναμη που τραβούσε τα αντικείμενα, αλλά το αποτέλεσμα της καμπύλωσης του ίδιου του χώρου και του χρόνου.
Ο φίλος και συνεργάτης του, Μαρσέλ Γκροσμάν, του υπέδειξε το έργο του Ρίμαν. Ο Αϊνστάιν ανακάλυψε ότι ο τετραδιάστατος χωροχρόνος δεν είναι τίποτα άλλο από μια Ριμάνια πολλαπλότητα. Τα μαθηματικά που περιέγραφαν καμπύλες επιφάνειες ήταν ακριβώς αυτά που χρειαζόταν για να εξηγήσει πώς η ύλη «λέει» στον χώρο πώς να καμπυλωθεί και πώς ο χώρος «λέει» στην ύλη πώς να κινηθεί. Χωρίς την πολλαπλότητα, η σύγχρονη φυσική θα ήταν αδύνατη.
Πέρα από τις τρεις διαστάσεις
Σήμερα, η έννοια της πολλαπλότητας έχει ξεπεράσει τα όρια της φυσικής και έχει εισχωρήσει σε πεδία που ο Ρίμαν δεν θα μπορούσε να φανταστεί.
Στη ρομποτική, οι κινήσεις ενός μηχανικού βραχίονα δεν υπολογίζονται απλώς στον τρισδιάστατο χώρο, αλλά σε μια «πολλαπλότητα διαμόρφωσης» πολλών διαστάσεων, που χαρτογραφεί κάθε πιθανή θέση και γωνία των αρθρώσεων.
Στην ανάλυση δεδομένων και τη μηχανική μάθηση, οι αλγόριθμοι προσπαθούν να βρουν μοτίβα σε ωκεανούς πληροφορίας. Η «Υπόθεση της Πολλαπλότητας» προτείνει ότι τα δεδομένα του πραγματικού κόσμου (όπως οι εικόνες προσώπων ή οι ήχοι ομιλίας), αν και φαίνονται χαοτικά και πολυδιάστατα, στην πραγματικότητα βρίσκονται πάνω σε δομές χαμηλότερων διαστάσεων που κρύβονται μέσα στον θόρυβο. Η κατανόηση αυτών των κρυμμένων σχημάτων είναι το κλειδί για την εκπαίδευση εξυπνότερων συστημάτων AI.
Ακόμη και στη Θεωρία των Χορδών, οι φυσικοί μιλούν για τις πολλαπλότητες Calabi-Yau, πολύπλοκα γεωμετρικά σχήματα έξι διαστάσεων που ίσως κρύβονται διπλωμένα μέσα στον ιστό της πραγματικότητάς μας, καθορίζοντας τους νόμους της φύσης.
Η κληρονομιά μιας ιδέας
Η διάλεξη του Ρίμαν τελείωσε με ένα θερμό χειροκρότημα, αλλά λίγοι τότε κατάλαβαν το μέγεθος της επανάστασης. Ο Γκάους, ωστόσο, αποχωρώντας από την αίθουσα, φέρεται να ήταν βαθιά εντυπωσιασμένος, αναγνωρίζοντας ότι ο μαθητής του είχε μόλις ανοίξει την πόρτα σε έναν νέο κόσμο.
Η πολλαπλότητα παραμένει μια από τις πιο ισχυρές έννοιες στην ιστορία της επιστήμης. Μας δίδαξε ότι για να κατανοήσουμε το μεγάλο και το περίπλοκο, πρέπει να κοιτάξουμε πώς συμπεριφέρεται το μικρό και το τοπικό. Από το σχήμα του Σύμπαντος μέχρι τη δομή της ανθρώπινης νοημοσύνης, όλα τελικά μπορεί να είναι απλώς ζήτημα γεωμετρίας.





